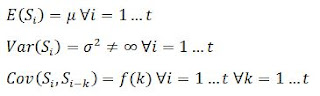Par : EL FAIZ Zakaria et ZOUIRI Sara
Master Recherche en Sciences Economique
UNIV. Mohammed V, FSJES Agdal.   
La modélisation des séries temporelles, nécessite, que ces dernières soient  stationnaires. Autrement dit que la série ne comporte ni tendance, ni cycle et ni saisonnalité. Cette notion de stationnarité représente un point crucial dans l’économétrie des séries temporelles, où l’estimation des séries non stationnaires conduit à des régressions fallacieuses ou illusoires. Pour éviter ces estimations fallacieuses, les économètres procèdent à la stationnarisation des séries chronologiques.
Régression fallacieuse
Régression exact
Une série temporelle est dite stationnaire si sa moyenne, sa variance et sa covariance sont constantes (ne sont pas affecté par le temps). Soit une série temporelle notée  à valeurs réelles et en temps discret. S est dite stationnaire (stationnarité du second ordre) si :
     
 
Ces conditions stipulent que l’espérance, la variance et la covariance sont constantes au cours du temps. A noter que la variance doit être finie. Si l’une de ces conditions n’est pas vérifiée, on parle donc de non stationnarité. Pour tester la non stationnarité des séries, on procède au test Augmented Dickey-Fuller. La stratégie de ce test est présentée comme suit :
 
Source : Boubonnais R., Econométrie : manuel et exercices corrigés, 9ème édition, Janvier 2015
Le test effectué sur le modèle 3 (voir figure ci-dessous) consiste à tester l’existence d’une tendance déterministe dans les séries. Autrement dit, tester l’hypothèse nulle qui stipule que ce coefficient associé à la tendance @trend est significativement égale à zéro. D’après la figure au-dessus, l’hypothèse nulle est acceptée pour les séries de la consommation nationale (CN) et du PIB. Par conséquent on décide l’absence d’une tendance déterministe pour ces deux processus. Cela est démontré par la significativité du coefficient de tendance @trend où le t-statistique des deux séries (CN et PIB) est inférieure à la valeur tabulée de la table de Student 1,96 (Respectivement 1,06 et 1,9). Nous passons au deuxième modèle dans lequel on test l’existence d’une tendance stochastique pour ces deux séries (CN et PIB).
Modèle 3
Log(CN)
Log(GOV)
Log(PIB)
La série des dépenses gouvernementales montre l’existence d’une tendance déterministe. La statistique de Student associée au coefficient @trend est égale à 2,06 qui est supérieur à la valeur critique de 1,96. On décide donc la non stationnarité de la série qui suit un processus DS puisque on admet l’hypothèse de présence e racine unitaire  avec une p-value de 0,57. On passe directement à la première différance de la série, est tester la stationnarité en suivant la même démarche (Modèle 1, Modèle 2 et Modèle 3)

Modèle 2
Log(CN)
Log(PIB)
 
La constante n’est pas significative pour la série de la consommation nationale (C=0 dans le schéma), puisque la p-value associée à  est supérieure au seuil critique de 0,05 avec 0,14. On conclut donc l’absence d’une tendance stochastique pour cette série. Pour le cas de la série du PIB, la constante est significativement différente de 0, puisque la p-value associé à  est inférieur 0,05 le seuil critique. A côté de cette constante on a la présence d’une racine unitaire, en fait, le processus autorégressif de ce processus est tester par   , la p-value associé à ce coefficient est égale à 0,08. On accepte donc l’hypothèse de non stationnarité du processus et on procède à sa différenciation. Pour la série de la consommation natioanle, on procède au test du processus autorégressif de la série ou comme appelé communément Random Walk à travers le modèle 1 .


Modèle 1
Log(CN)



L’hypothèse nulle de ce test correspond à tester l’existence de racine unitaire dans le processus. Les résultats du test nous informe qu’on ne peut pas rejette l’hypothèse nulle d’existence de racine unitaire puisque la statistique de Augmented Dickey-Fuller calculée est supérieure à la valeur critique de la table ADF (8,24>-1,94). Les séries de la consommation nationale est par conséquent non stationnaire et suit un processus DS.
Comme indiqué, pour stationnarité nos séries, on doit procéder à la différence première pour annuler la tendance déterministe de la série des dépenses gouvernementale, annulées le Random Walk avec dérive de la série du PIB, et le Random Walk de la série de la consommation nationale.
Les graphs des séries en première différence sont présentés comme suit :

D(Log(CN))
D(Log(GOV))


D(Log(PIB))

En exécutant le test de stationnarité ADF, de la même manière sur les séries en différence comme démontré sur les séries en niveau (Modèle 3, Modèle 2 et modèle 1), nous indique que tous les variables sont stationnaires et nécessite pas une deuxième différence.
En récapitulant, pour modéliser le comportement d’une série chronologique, il faut neutraliser les séries de la saisonnalité, tester la stationnarité des séries en niveau. Si le test de stationnarité montre l’existence d'une racine unitaire, il faut soustraire la tendance si la composante tendancielle est déterministe, différencier la série si la série représente une marche aléatoire avec ou sans dérive. Dans ce qui va suivre, on va procéder à la modélisation univariée d’une série chronologique à travers les modèles AR (p), MA (q), ARMA(p,q), ARIMA(p,d,q)…, ensuite la modélisation multivariée à travers les modèles VECM et VAR.
Par : EL FAIZ Zakaria et ZOUIRI Sara
Master Recherche en Sciences Economique
UNIV. Mohammed V, FSJES Agdal.
 
Pour estimer la tendance d’une série chronologique on peut procéder par trois méthodes. La première consiste à calculer une  moyenne mobile selon un ordre déterminé à priori ou a postériori, ou analytiquement par estimation d’une droite en régressant la série sur la période qu’elle couvre, ou par filtration (filtre HP, Kalman,…).

Estimation de la tendance par la méthode de la moyenne mobile 

Pour appliquer la méthode de la moyenne mobile il faut disposer d’une série assez longue qui peut résister à une perte d’information. Cette méthode procède à une transformation des données en moyenne d’un ordre (p) choisi à priori en fonction du degré de lissage de la série voulue.
 
Pour notre cas, on choisit de transformer les données en moyenne mobile d’ordre 4, puisqu’elles sont exprimées en fréquences trimestrielles. La quantité d’observations perdues de chaque extrême est égale à k=P/2 si l’ordre de la moyenne (p) est paire. k=(P-1)/2 si l’ordre est impaire. Dans notre cas, on aura une perte de 2 observations de chaque extrême (la quantité d’information perdue  est  de 4 observations). 
 
La 3ème observation de notre série est calculée avec la formule ((120/2)+181+71+119+(128/2))/4, et comme formule générale on a :
 
Les tendances des trois séries sont présentées en rouge sur la figure ci-après :
 
GOV
CN
PIB


Commande sur Eviews : genr series = @movav(cn01,4)

 

Estimation de la tendance analytiquement

A l’aide de Eviews 9, on estime la tendance de la série du PIB, pour ce faire, on régresse notre série sur le temps (1, 2, 3,…,T) et une constante. Les résultats de cette estimation sont résumés dans le tableau suivant :
GOV
CN


PIB

 

Commande sur Eviews : ls pib c @trend

On remarque que la constante et le trend sont significativement différents de zéro pour toutes les équations, ce qui confirme l’existence de la tendance. La représentation graphique de ces trois équations est représentée en rouge sur les graphs suivants :

GOV
CN
PIB

 

Commande sur Eviews : plot pib pib_trend

Formulaire de contact

Nom

E-mail *

Message *